挑战408——组成原理(1)——看看我们要学什么
计算机的发展历程
我一直觉得,要想深入理解,学习一门课程,就必须了解一下它的发展史,尤其是计算机发展对比其他的专业来说可以说是相当的晚了。才100多年历史。所以有机会我一定要好好看看这100年计算机都发生了什么。 言归正传。世界上第一台计算机是1946年在美国诞生的ENIAC。1945年,冯诺依曼提出了存储程序的思想:必须将事先编好的原始程序和数据一同送入主存后,才能执行程序,一旦程序被执行,计算机能在无须人工操作的干预下,自动完成逐条取出指令,并执行的任务。 1965年,Intle公司的缔造者Gordon提出,“微芯片上的集成的晶体管数目,每三年番2倍”的规律,这就是著名的摩尔定律。
硬件发展带来的问题
微处理器的发展,几乎每3年,处理器的性能就提高4—5倍,但计算机上的一些其他部位性能提高的速度达不到该水平 。影响不同部件性能不匹配的主要处理因素为CPU与主存间接口和CPU与外设的接口问题,具体体现在: - CPU与主存之间:是整个计算机最重要的通路,负责在主存和处理器之间传送指令和数据。试想如果与CPU之间的数据传送跟不上CPU的要求,那么CPU就会处于等待状态。一般的我们采取如下方式进行处理: - 加宽数据总线的宽度(道路太挤,扩宽一下) - 在两者之间设置高速缓存(Cache,先给CPU提前准备好原料),并发展为片内缓存和分级缓存。 - 利用高速连接总线和分层总线,来缓冲和分流数据。以提高处理器与存储器之间的连接宽带。 - CPU与外设之间的接口:常见的处理方式: - 加入缓冲机制 - 用高速互连总线以及更快的总线结构来解决。
这些问题都是硬件发展中带来的问题,也是这门课程重点讨论的问题。下面介绍一下软件的发展历程。个人认为仅做了解即可。
软件的发展
软件技术的发展主要体现在编程语言之间的进步。编程语言大致经历了如下的阶段: 机器语言(0 1 代码)——>汇编语言(与机器语言对应)——>高级语言(C++,JAVA)而高级语言不能直接运行,而是需要由程序翻译成机器语言,所以将高级语言程序翻译为机器语言程序的软件,称为翻译程序。而翻译程序又根据翻译形式的不同,分为两种形式: - 编译程序:先把所有的程序都全部翻译完,再执行 - 解释程序:翻译一次,执行一次,边翻译边执行
计算机系统的层次结构
先上图:
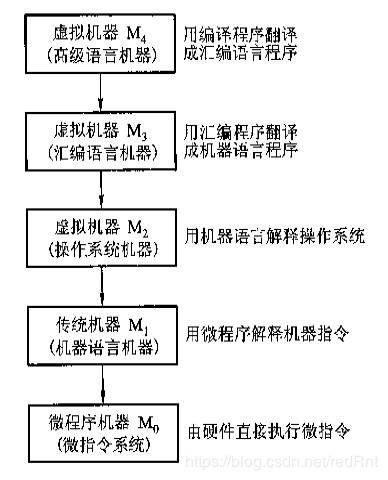
说白了,这个体系就分为两个部分,软件范围(M4 - M 2)和硬件范围(M1-M0).而软件与硬件之间需要有一个桥梁,以便软件和硬件能相互合作,交互。这个桥梁位于 M2和M1之间,这个桥梁称为指令集体结构(ISA)。也就是说,软件与硬件的交互是通过指令来进行的。
典型的冯诺依曼体系结构及其特点
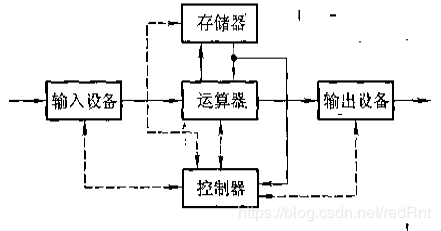
机器以运算器为中心。I/O设备与存储器之间的数据传送通过运算器完成 2. 计算机由运算器,控制器,存储器,I/O设备 五大部件组成。 3. 指令和数据地位相同,按地址访问,按顺序存放
PS:这门课程就是以2为主线,讲解计算机的组成原理的。
计算机软件的分类
一般的我们将计算机软件分为:系统软件和应用软件。其中系统软件包括操作系统,数据库管理系统,语言处理系统等等。
计算机的性能指标
机器字长:指CPU一次能处理的数据的位数。字长越长,数的表示范围越大,精度越高
存储容量:包括主存和辅存容量。具体的到讲了存储器再说。
运算速度:
MIPS:单位时间内执行指令的平均条数
CPI:执行一条指令所需要的时钟周期
FLOPS:每秒的浮点数运算的次数
最常见的问题:指令和数据如何区分?
挑战408——组成原理(2)——二进制数和十六进制数
这算是数据的表示运算这一部分的第一篇文章了,这部分多且繁杂,因为我们通常都是以10进制的数进行计算和表示的,用了10几年,突然接受一种新的表示方式难免会导致理解困难。初学这章我也是半懵逼状态的,好在复习了一轮后,又去多次问了老师相应的问题,才算有个大致的了解。所以这系列的文章如果有不对的地方,欢迎批评指正。
这篇是基础篇,是学习后面的各种运算的基础,所以得好好看,好好理解。
从10进制->2进制->16进制
我们的日常习惯,是用10进制表示的,如果满10了就向前进一位。比如 9 + 2 = 11. 9 + 2 = 10 + 1,所以向前进一位,剩下的位数填在后面。
那么好端端的为什么我们在机器中不用10进制表示而非要改变常规的思路使用二进制呢?我们当然不是吃饱了撑的,是没办法的事,因为这是由计算机的硬件决定的(可以多去百度,不细说)。在接下来的学习中,10进制到2进制的转换就是家常便饭了。具体的转换规则我想打算考408的不可能不会,所以不说。
类似的,计算机也常有16进制来表示一些数,如果说二进制是为了让计算机更容易理解我们的10进制表达方式,那么16进制就是为了让我们更容易读懂计算机的表达方式,而且利用16进制数可以快速的在2进制和16进制之间相互转化。(因为4位2进制数恰好可以表示16个数字(即0-15))。16进制数最常用的是在表示物理内存空间的时候,比如我们看到的0xAFFFH等等就是典型的16进制数。
BCD编码
为了方便的表示各二进制与其他进制的转换关系,于是有了BCD编码,编码的种类很多,我们就讲最简单,最常用的8421编码。特点是用4位二进制数表示一位16进制的数。
下面的表列出了8421编码的对应项(完全可以自己手动算,要记住下面的这个内容):
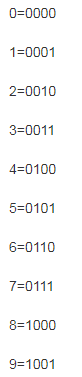

为什么强调这张表的重要性呢?我们看看怎么转换吧:
比如,给出一个16进制的数036A,我们化为二进制数就可以这样化:
从末尾开始,将每个16进制的位数都按照形式相应的写出二进制数。
拼接即可。
所以,直接写出二进制数为:
0000,0011,0110,1010(是不是特别方便?这里的逗号是为了方便观察而加的,实际不存在)。
挑战408——组成原理(3)——原码,补码,反码
计算机中的数据分为数值数据和非数值型数据(如声音,图像等等)。我们接下来主要谈的是数值型数据。
在现实的生活中,数值数据主要分为实数和整数两大类,在计算机中,整数用定点数表示,实数用浮点数表示,而所有带符号的整形都用补码表示。目前通用计算机中浮点数大多数采用IEEE754标准,其中尾数采用定点原码表示,所以浮点数的算术运算涉及原码的加减乘除运算。
无符号数与有符号数
无符号数,即没有正负号的数,是数的绝对值,在其面前添上正负号,便成了有符号的数。计算机的数均存放在寄存器中,通常我们称寄存器的位数为机器字长,当存放有符号数的时候,需要占用以为存放符合位,所有,如若机器字长为16位,那么:
无符号数可表示的范围为 0 — 2^(16) -1
有符号数可表示的范围为 -2^15 — 2^(15) - 1
15次方是因为符号位占用了一位。
那么计算机如何表示有符号数呢?我们规定,用0表示正号,用1表示负号,这样符号也就被数字化了,并规定放在有效数据之前,例如:
+0.1011 在机器中表示为0(小数点位置)1011
-1100 在机器中表示为1,1100(小数点位置)
为了方便区分手写的数和将符号数字化的数,我们把前者称为真值,后者称为机器数。即
-1100(真值) -> 11100(机器数)
将符号数字化以后带来了新的问题,运算时,符号位是否参与运算,如果是,那么如何处理?为了处理好这些问题,于是就引入了原码,补码,反码和移码等编码方式。
原码
原码,又称带符号的绝对值表示,符号位为0表示正,为1表示负。用大白话来讲,就是直接将数值部分写成二进制数然后前面添上0或者1,用来表示正负号。
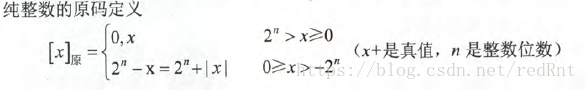
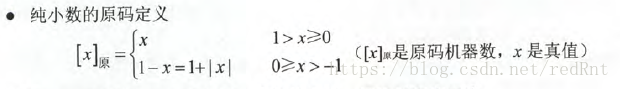
其实上面的公式我们只需要了解即可,实际的转换很简单
比如X = +1110时 [X]原 = 0,1110
X = -1110时 [X]原 = 1,1110 (逗号只是为了区分符号位实际不存在)
X = 0.1101时 [X]原 = 0.1101
X = -0.1101时 [X]原 = 1,1110(注意不是10.1101,因为0并不是有效数据位)。
注意: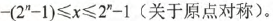
若字长为n+1,那么原码整数的表示范围为:
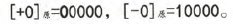
原码中0的表示方式有两种:
补码
如果说是这几种码制中最重要的编码方式,一点也不为过。计算机中存放的数值方式大多数是用补码存放,计算(尤其是减法做加法运算时)时也通常采用补码运算方式,因此要对补码非常敏感。
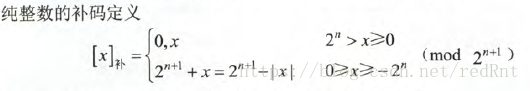
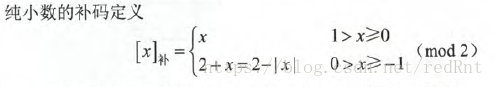
对于纯整数: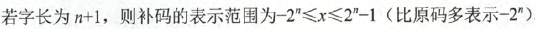
对于纯小数:
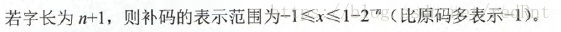
而对于0而言,
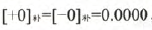
具体的实例不举先,先看看我们的反码,我们没有必要按上面的数学公式往上套。
反码
反码,通常用来由原码求补码或者由补码求原码的过渡环节。
我们先看看数学定义:
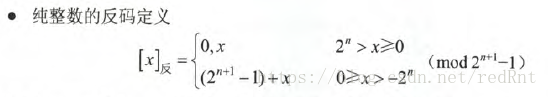
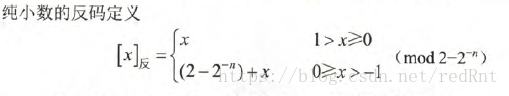
对于纯小数:
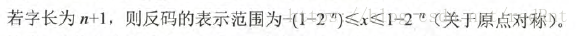
对于纯整数:
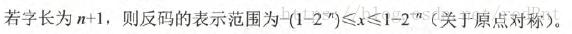
所以,记住上面的就够了,我们具体看看运算过程,取反操作就是将原码中的0换成1,1换成0.就完事了。
当X = +1101时,X反 = 0,1101
当X = -1101时,X反 = 1,0010(当为负数的时候,符号位不变,数值位执行取反操作)
当X = +0.0110时,X反 = 0.0110
当X = -0.0110时,X反 = 1.1001
对于0来说,反码的表示方式也有两种(0,000或者1,111),这就自己去写了。
三种码制之间的关系(最重要)
前面的数学公式是应付表示范围类的题目,那么这些内容就是应付计算题的题目:
三种机器码的最高位均为符号位,符号位与数值位用逗号隔开
当真值为正时,原码补码反码表示方式相同。
当真值为负时,三者表现都不同,但是符号位都用1表示,补码可以用“原码求反(不含符号位)后加1”求得。而反码是原码除了符号位以外的部分都进行取反操作。
下面举个简单的计算例子:
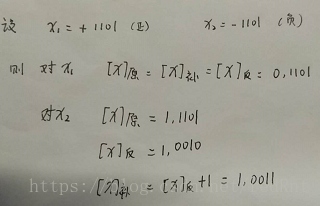
移码
当真值用补码表示的时候,由于符号位与数值位一起编码,这与习惯上表示不同,我们很难从补码形式上直接判断真值的大小。但是如果对每个真值位(注意不包含符号位),都加上一个2^n(n为整数位),那么在数轴上,移码表示的范围恰好对应真值在数轴上移动2的n次方个单元。所以叫做移码。
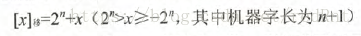
它常常用来表示浮点数的阶数,因为它只能表示整数。
对于移码来说,0的表示是唯一的,假设字长为6位(含一个符号位)那么0的表示为:
+0移 = (2^5) + 0 =1,00000
-0移 = (2^5) - 0 =1,00000
特点:
0 的表示方式唯一
对于同一个真值,移码和补码相差一个符号位,且相反,例如:-11110 补码为1,00010,移码为:000010
引入移码是为了直观的判断真值大小,所以移码大,真值就大

