title: 计算机组成原理
categories:
- CS基础
tags: - 计组
- 专业课
- 笔记
- 基础
typora-root-url: ..
计算机组成原理
预备知识
进制知识
数电逻辑

计算机中阶符、阶码、数符、尾数的意思
一个浮点数a由两个数m和e来表示:a = m × b^e。在任意一个这样的系统中,我们选择一个基数b(记数系统的基)和精度p(即使用多少位来存储)。m(即尾数)是形如±d.ddd…ddd的p位数(每一位是一个介于0到b-1之间的整数,包括0和b-1)。如果m的第一位是非0整数,m称作规格化的。有一些描述使用一个单独的符号位(s 代表+或者-)来表示正负,这样m必须是正的。e是指数。
结构
由此可以看出,在计算机中表示一个浮点数,其结构如下:
尾数部分(定点小数) 阶码部分(定点整数)
一个十进制数可写成一个纯小数乘上10的若干次方,相似的,一个二进制可写成一个纯小数乘上2的若干次方。例如,11.01=22×0.1101;
一般地,任一个二进制N,可表示为N=2j×S;
其中J为二进制数,叫阶码;
J如果有正负号的话,正负号就叫阶符;
S为纯小数,叫做尾数;
数符,指的是N整个数的符号。
浮点数能表示的范围由阶码的位数决定,精确度有尾数的位数决定
————————————————
版权声明:本文为CSDN博主「猴儿2333」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/littlecase233/article/details/82959410
在尾数用补码表示时,规格化浮点数应满足尾数最高数位与符号位不同,如相同就是不满足规格化。
尾数用双符号位补码表示,经过加/减运算之后,可能出现以下六种情况,即
① 00.1 x x … x
② 11.0 x x … x
③ 00.0 x x … x
④ 11.1 x x … x
⑤ 01.x x x … x
⑥ 10.x x x … x 第①、②种情况,符合规格化数的定义,已是规格化数。 第③、④种情况不是规格化数,需要使尾数左移以实现规格化,这个过程称为左规。尾
浮点数运算的的规格化
浮点数运算的的规格化
浮点数运算的的规格化
数每左移一位,阶码相应减 1,直至成为规格化数为止。
左规可以进行多次。
第⑤、⑥种情况在定点加减运算中称为溢出,但在浮点加减运算中,只表明此时尾数的 绝对值大于 1,而并非真正的溢出。这种情况应将尾数右移以实现规格化。这个过程称为右 规。尾数每右移一位,阶码相应加 1。
右规最多只有一次。
总结:左规处理,及时数往小数点左边走,阶码-1,右规反之。
https://blog.csdn.net/qq546770908/article/details/45486397
小数的二进制表示,阶码
知识点 加 题目 加 排版 加 图片 加 个人思想
第1章 计算机系统概率
1.1 计算机的分类
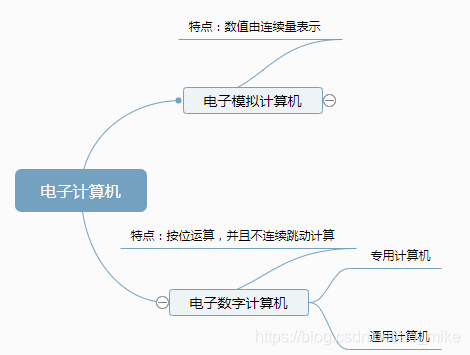


1.2 计算机的发展简史
已知补码如何求原码(真值)~
1.当补码最高位为0时
因为最高位为0,即该数是正数,正数的原码、反码、补码都是一样的。
所以该补码即是原码。
例如:【X】补=01111111求真值。
解:因为最高位为0,所以【X】原=【X】补=01111111=127.
2.当补码最高位为1时
因为最高位是1,所以该数为负数。负数的补码=反码+1
补码 的补码 即为该补码的原码(真值)。
逻辑右移就是不考虑符号位,右移一位,左边补零即可。
算术右移需要考虑符号位,右移一位,若符号位为1,就在左边补1,;否则,就补0。
所以算术右移也可以进行有符号位的除法,右移,n位就等于除2的n次方。
例如,8位二进制数11001101分别右移一位。
逻辑右移就是[0]1100110
算术右移就是[1]1100110

